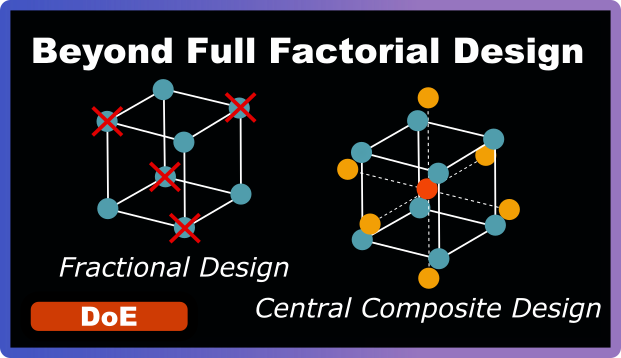
Introducing Fractional & Central Composite Designs
When it comes to experimental design, full factorial designs are often the starting point. They’re straightforward, systematic, and provide a complete picture of the interactions between factors. However, as the number of factors increases or when optimization is the goal, full factorial designs can quickly become impractical. In these situations, fractional factorial designs and central composite designs (CCDs) are often better suited.
The Challenge with Full Factorial Designs
Imagine you’re developing a new coating formulation and suspect that temperature, humidity, coating thickness, curing time, and substrate material all affect adhesion strength. A full factorial design would require 32 experiments just to test these 5 factors at 2 levels each. Add solvent type as a sixth factor, and you’re suddenly looking at 64 experiments. For many projects, especially in the early screening phase, this isn’t just expensive—it’s unnecessary. Most of those 64 experiments are testing high-order interactions that rarely matter in practice.
Fractional Factorial Designs: Efficient Screening
Fractional factorial designs tackle this by strategically selecting a subset of the full factorial experiments. Instead of running all 32 experiments for your 5-factor coating study, you might run just 16 (a half-fraction) or even 8 experiments (a quarter-fraction).
The Trade-off: Information vs. Efficiency
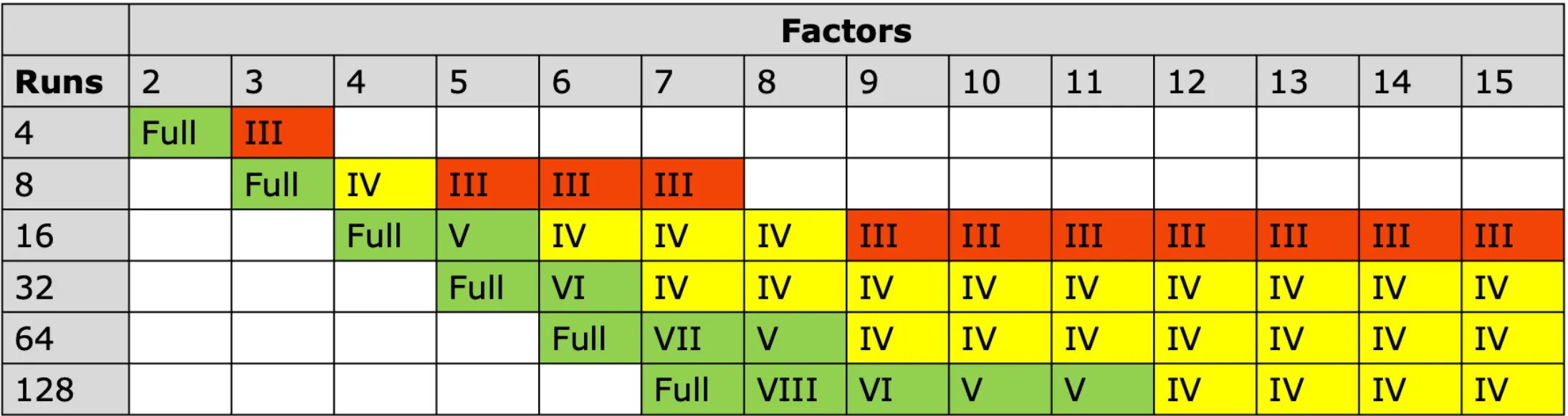
Here’s what you’re trading off: fractional designs can’t separate certain effects from each other—we call this “confounding” or “aliasing.” How severe this confounding is depends on the design resolution, which is determined by both the number of factors and the size of the fraction you choose. In a Resolution III design (common with quarter-fractions or smaller), main effects are confounded with two-factor interactions — a significant limitation. Resolution IV designs keep main effects clear but confound two-factor interactions with each other. Resolution V designs maintain separation between main effects and two-factor interactions, confounding only higher-order interactions.
But the key point is this: in most real-world systems, higher-order interactions are either negligible or much smaller than main effects, making even Resolution IV designs quite practical for screening experiments and Resolution V designs often as powerful as full factorial designs.
Fractional designs are especially useful in the early stages of research and development. At this stage, the goal is often to identify the key factors that significantly impact the outcome. By focusing on main effects and lower-order interactions, fractional designs provide a “compass” to guide further investigation. They’re not just efficient; they’re scalable. If more detailed information is needed later, the design can be extended to a full factorial.
When Fractional Designs Make Sense
Fractional factorial designs are a great choice when:
- You’re in the screening phase with many potential factors
- Resources (time, materials, budget) are limited
- You suspect only a few factors will be truly important
Moving Beyond Linear Relationships: Central Composite Designs
Both full and fractional factorial designs typically use just two levels per factor. This works well for screening and understanding linear relationships, but what happens when you need to find an optimum? Linear models can tell you which direction is better, but they can’t locate a peak or valley in your response surface. Central composite designs (CCDs) address this limitation by adding two types of points to a base factorial design:
- Center points: Experiments run at the middle level of all factors
- Star points: Experiments run at extended high and low levels beyond the original factorial range

Visualizing the Design Space
If you think of a 3-factor experiment as a cube, a standard 2-level factorial design places experiments only at the cube’s corners. A CCD adds experiments at the cube’s center and extends out to points on the faces (or beyond), creating a more comprehensive exploration of the design space. This expanded design allows you to fit quadratic models, which can capture curvature in your response surface—essential for finding optimal operating conditions.
You could achieve the same with 3-level full factorial designs, but you would need to run many more experiments.
For example: Your initial screening (perhaps using a fractional factorial) identified three critical factors: compression force, dwell time, and lubricant concentration. You know these factors matter, but now you need to find the optimal settings. A 3-factor CCD might include:
- 8 factorial points (the corners of your design cube)
- 6 star points (extending beyond the cube faces)
- 1 center point (right in the center of the cube)
With just 15 experiments (compared to 27 for a 3-level full factorial), you can fit a quadratic model that reveals not just which factors matter, but exactly where your optimum is.
Choosing the Right Design for Your Goals
The key is matching your design choice to your research stage and objectives:
Start with fractional factorial when you have many potential factors and need to identify which ones actually matter. Use it as a compass. Maybe you can eliminate some factors as you find they are not important or you learn that you need to adapt the ranges you are testing. You can comfortably choose a resolution IV design. If you have many factors, you can also go with a resolution III design, but be careful as two-way interactions are aliased with main effects and both can be quite important.
Consider full factorial designs when you have a manageable number of factors (typically 4 or fewer). Then the number of experiments is still manageable. Also, after your initial screening, if you are unsure about your interactions due to aliasing, you can use a full factorial design to resolve the interactions and get a clear picture. If you can perform a resolution V fractional design, do it and skip the full factorial design entirely. It will be fine.
Move to central composite designs once you’ve identified your key factors and need to optimize. This is your precision phase — you’re fine-tuning your process to find the sweet spot. It always comes at the end. Never start with a central composite design.
Practical Implementation Tips
For fractional designs:
- Resolution IV designs are a good choice for screening. You can estimate main effects (almost) independently and already get some information about interactions
- Use resolution V designs when possible—they keep main effects and two-factor interactions unconfounded
- Plan for follow-up experiments to resolve any important confounded effects
For CCDs:
- Use rotatable designs when you want equal prediction precision in all directions from the center
- Include adequate center point replicates to estimate pure error
- Consider the practical feasibility of your star point settings—they extend beyond your original factor ranges
For both approaches:
- Randomize your experimental run order to minimize the impact of lurking variables
- Consider blocking strategies if experiments must be run over multiple days or with different operators
- Always validate your models with confirmation experiments at predicted optimal conditions