This guide walks you through creating fractional factorial designs using Python’s pyDOE3 package. I won’t cover the theory of what fractional designs are or how they work—if you need that background, check out these articles first:

• Introducing Fractional & Central Composite Designs
• Example of a Fractional Factorial Design

Installation and Setup

First, install the required packages. If you already followed the full factorial design tutorial, you can skip this step:

pip install pydoe3 pandas numpy

Next, import the packages:

from pydoe3 import fracfact, fracfact_opt, fracfact_by_res
import pandas as pd
import numpy as np

The pyDOE3 package gives you three main functions for fractional factorial designs: fracfact() for manual generator strings, fracfact_opt() for automatically finding optimal designs, and fracfact_by_res() for specifying design resolution directly. Each approach works best in different situations depending on how much control you need.

Create a fractional design with a generator string

Basic 2^(3-1) Design

Let’s start with a simple example. Suppose you have 3 factors (A, B, C) but want to run only 4 experiments instead of the full 8:

# Create a 2^(3-1) fractional factorial design
design = fracfact('a b ab')
print(design)

Output:

[[-1. -1.  1.]
 [ 1. -1. -1.]
 [-1.  1. -1.]
 [ 1.  1.  1.]]

In the generator string 'a b ab', factors A and B are independent (they can take any combination of -1 and +1), while factor C is generated as the product of A × B. That’s why the third column shows +1 when A×B = (-1)×(-1) = +1 or A×B = (+1)×(+1) = +1, and -1 when A×B = (+1)×(-1) = -1 or A×B = (-1)×(+1) = -1.

This creates the alias structure: C = AB. The main effect of factor C is confounded with the AB interaction. You’ll measure both effects combined, but you can’t separate them.

The complete alias structure for this Resolution III design is:

• A = BC (main effect A confounded with BC interaction)
• B = AC (main effect B confounded with AC interaction)
• C = AB (main effect C confounded with AB interaction)

You’re looking at a Resolution III design. In Resolution III designs, main effects are confounded with two-way interactions, making them suitable for screening experiments where you assume interactions are negligible.

Example: the 2^(4-1) Design from our Filtration Rate Study

Now let’s tackle something more practical. We’ll recreate the 2^(4-1) fractional design from our fractional factorial post using pyDOE3. We have 4 factors but want to run only 8 experiments instead of 16—cutting our experimental cost in half. For a 2^(4-1) design, we need a generator that creates the 4th factor from the first three:

# Create a 2^(4-1) fractional factorial design
# Generator: 'd = abc' (4th factor = product of first three)
design = fracfact('a b c abc')

To make the output more practical, we convert it to a DataFrame with meaningful column names:

# Convert to DataFrame with meaningful names
factors = ['Temperature', 'Pressure', 'Concentration', 'RPM']
df = pd.DataFrame(design, columns=factors)
print(df)

Output:

	Temperature	Pressure	Concentration	RPM
0	-1.0	-1.0	-1.0	-1.0
1	1.0	-1.0	-1.0	1.0
2	-1.0	1.0	-1.0	1.0
3	1.0	1.0	-1.0	-1.0
4	-1.0	-1.0	1.0	1.0
5	1.0	-1.0	1.0	-1.0
6	-1.0	1.0	1.0	-1.0
7	1.0	1.0	1.0	1.0

Notice how the RPM column is created by multiplying Temperature × Pressure × Concentration.

Note: A 2^(k–1) design is called a half fraction (half the runs of the full factorial). A common generator pattern defines the last factor as the product of the previous ones (e.g., for four factors: a b c d=abc; for five: a b c d e=abcd). Other generators exist, but if you want minimal confounding, this is usually your best choice.

You can also convert these coded values to actual experimental settings:

# Define the actual factor levels
factor_levels = {
    "Temperature": (70, 90),    # °C
    "Pressure": (25, 35),       # psi  
    "Concentration": (2, 6),    # %
    "RPM": (150, 200)          # rpm
}

# Map coded values to real values
for factor, (low, high) in factor_levels.items():
    df[factor] = df[factor].map({-1: low, 1: high})

print(df)

Result:

	Temperature	Pressure	Concentration	RPM
0	70	25	2	150
1	90	25	2	200
2	70	35	2	200
3	90	35	2	150
4	70	25	6	200
5	90	25	6	150
6	70	35	6	150
7	90	35	6	200

More complex generator strings

As your experiments grow more complex, you can create more aggressive fractional designs. Here are some examples:

Quarter Fraction: 2^(5-2) Design

For 5 factors with only 8 runs (quarter of the full 32 runs):

# Create a 2^(5-2) fractional factorial design
# Generators: D = AB, E = AC
design = fracfact('a b c ab ac')
print(f"Design shape: {design.shape}")

This uses two generators (AB and AC), creating a quarter fraction with 8 runs instead of 32.

High-Factor Screening: 2^(7-4) Design

For screening 7 factors with only 8 runs (Resolution III):

# Create a 2^(7-4) fractional factorial design for screening
design = fracfact('a b c ab ac bc abc')
print(design.shape)

The generators offer good customization since you control which factors are confounded. This helps when you already know that certain interactions are unlikely or impossible. For example, in a chemical process, you might know that pH (factor A) and stirring speed (factor B) can’t physically interact with catalyst type (factor C) and reaction temperature (factor D). In this case, you could strategically choose generators like D = AC and E = BC to avoid confounding the pH-stirring interaction with anything important.

However, working with generators can become quite complex, and sometimes you just want the best solution with minimal confounding or a design with a certain resolution. For these situations, pyDOE3 offers two easier approaches: fracfact_opt() for finding optimal confounding patterns automatically, and fracfact_by_res() for directly specifying the design resolution you need.

Finding optimal designs with fracfact_opt

When you have multiple ways to create a fractional design, fracfact_opt() helps you pick the one with the highest resolution by scanning all possible generator combinations and selecting the one with minimal confounding:

# Find the optimal generator for a 2^(6-2) design
# (6 factors, 2 generators, 16 runs instead of 64)
design_string, alias_map, alias_cost = fracfact_opt(6, 2)

print(f"Optimal generator string: {design_string}")
print("First few alias relationships:")
for i, alias in enumerate(alias_map[:5]):
    print(f"  {alias}")

Let’s break down what this function returns:

• design_string: The optimal generator string (e.g., “a b c d ab ac”) ready to use with fracfact()
• alias_map: A list showing which effects are confounded with each other
• alias_cost: A numerical score indicating confounding severity (lower is better)

The function automatically tests different generator combinations and picks the one that creates the least problematic confounding. For example, it prefers designs where main effects are confounded with higher-order interactions rather than other main effects.

You can then create your design using the optimal generator:

# Use the optimal generator to create the actual design
optimal_design = fracfact(design_string)
print(f"Created {optimal_design.shape[0]} runs for {optimal_design.shape[1]} factors")

Quick design generation with fracfact_by_res

When you know the resolution you need but don’t want to figure out the generator string, use fracfact_by_res():

# Create a 6-factor Resolution III design (minimal confounding for screening)
design_res3 = fracfact_by_res(6, 3)
print(f"Resolution III design shape: {design_res3.shape}")

# Create a 6-factor Resolution IV design (better for main effects)
design_res4 = fracfact_by_res(6, 4) 
print(f"Resolution IV design shape: {design_res4.shape}")

This function takes two parameters: the number of factors and the desired resolution. It automatically determines the minimum number of runs needed and creates an appropriate design.

Notice how the Resolution IV design requires more runs than Resolution III—this reflects the trade-off between experimental cost and information quality. The function automatically balances this for you based on your specified resolution requirement.

This approach works particularly well when you’re working within budget constraints (“I can afford 32 runs maximum”) or quality requirements (“I need all main effects to be clear of two-way interactions”).

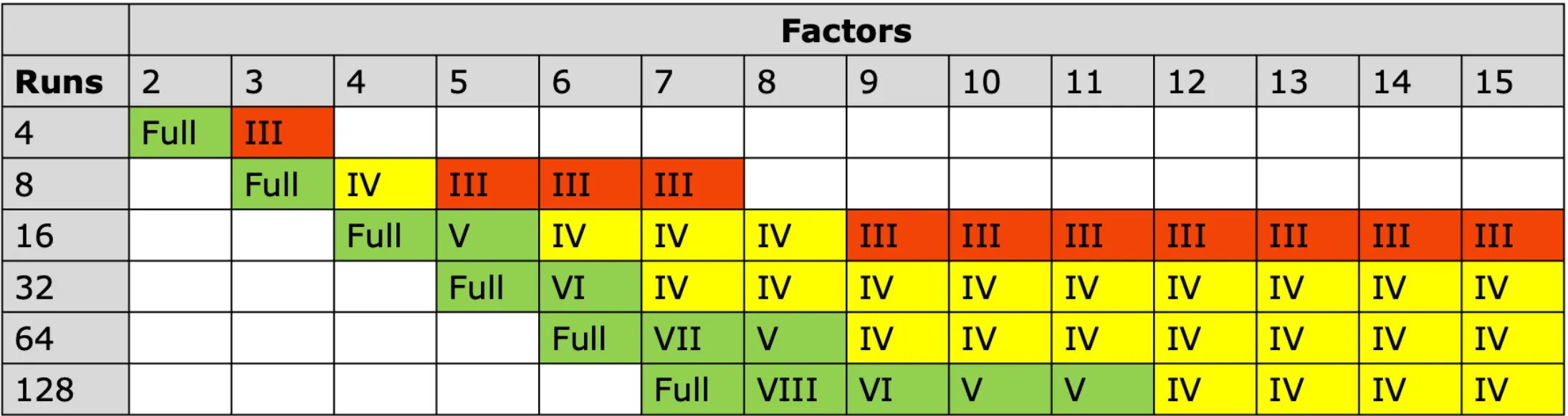
Resolution guide:

• Resolution III: Main effects confounded with two-way interactions (screening only)
• Resolution IV: Main effects clear, two-way interactions confounded with each other (most common)
• Resolution V: Main effects and two-way interactions clear (nearly as good as full factorial)

Here’s an overview table for design resolution:

Quick reference: Copy-paste templates

Basic fractional factorial template

from pydoe3 import fracfact
import pandas as pd

# 1. DEFINE YOUR FACTORS (edit these for your experiment)
factors = {
    "Factor_A": (low_value, high_value),
    "Factor_B": (low_value, high_value), 
    "Factor_C": (low_value, high_value),
    "Factor_D": (low_value, high_value)
}

# 2. CREATE FRACTIONAL DESIGN 
design = fracfact('a b c abc')  # Edit generator string as needed

# 3. CONVERT TO DATAFRAME
df = pd.DataFrame(design, columns=factors.keys())

# 4. MAP TO REAL VALUES
for factor, (low, high) in factors.items():
    df[factor] = df[factor].map({-1: low, 1: high})

# 5. RANDOMIZE AND EXPORT
df = df.sample(frac=1, random_state=42).reset_index(drop=True)
df.index += 1
df.index.name = 'Run'
df['Result'] = ''
df.to_excel('fractional_experiment.xlsx')
print(f"Design created: {len(df)} runs")

Optimal designs

from pydoe3 import fracfact_opt, fracfact_by_res
import pandas as pd

# 1. DEFINE EXPERIMENT PARAMETERS
num_factors = 6
num_generators = 2  # This gives 2^(6-2) = 16 runs instead of 64

# 2. FIND OPTIMAL DESIGN
optimal_generator, aliases, cost = fracfact_opt(num_factors, num_generators)
print(f"Optimal generator: {optimal_generator}")

# 3. CREATE DESIGN
design = fracfact(optimal_generator)

# 4. REST OF WORKFLOW
# ... (same as basic template)

Designs by resolution

from pydoe3 import fracfact_by_res
import pandas as pd

# 1. DEFINE EXPERIMENT PARAMETERS
num_factors = 5
resolution = 4  # Resolution IV ensures main effects are clear

# 2. CREATE DESIGN BY RESOLUTION
design = fracfact_by_res(num_factors, resolution)
print(f"Created Resolution {resolution} design: {design.shape[0]} runs for {num_factors} factors")

# 3. CONVERT TO DATAFRAME WITH MEANINGFUL NAMES
factor_names = [f"Factor_{chr(65+i)}" for i in range(num_factors)]  # A, B, C, D, E
df = pd.DataFrame(design, columns=factor_names)

# 4. MAP TO REAL VALUES (customize these ranges)
factor_levels = {name: (0, 100) for name in factor_names}  # Example: 0-100 range
for factor, (low, high) in factor_levels.items():
    df[factor] = df[factor].map({-1: low, 1: high})

# 5. EXPORT FOR EXPERIMENTATION
df.index += 1
df.index.name = 'Run'
df['Result'] = ''
df.to_excel(f'resolution_{resolution}_design.xlsx')
print(f"Design exported: {len(df)} runs")

Key takeaways

Generator strings (fracfact()): Use when you need precise control over which factors are confounded. Best for experts who understand the alias structure and want to customize confounding patterns based on domain knowledge (e.g., knowing certain interactions are impossible). Requires understanding of generator notation but offers maximum flexibility.

Optimal designs (fracfact_opt()): Use when you want the best possible design for a given number of factors and runs, but don’t want to figure out the generators manually. The algorithm finds the highest resolution design possible, automatically minimizing problematic confounding. Perfect for getting quality designs without deep DOE expertise.

Designs by resolution (fracfact_by_res()): Use when you know the quality level you need (Resolution III for screening, IV for main effects, V for interactions) but want the algorithm to determine the minimum number of runs required. Best for budget-driven decisions where you need to balance experimental cost with information quality.

Up next:

<< Mathematical Models in DOE >>

<< How to perform ANOVA >>